学术信息网 西电导航 关于 使用说明 搜索 系统首页 登录 控制面板 收藏 陈琦的留言板
理论类型课题：

  1. 熵区域的刻画问题：

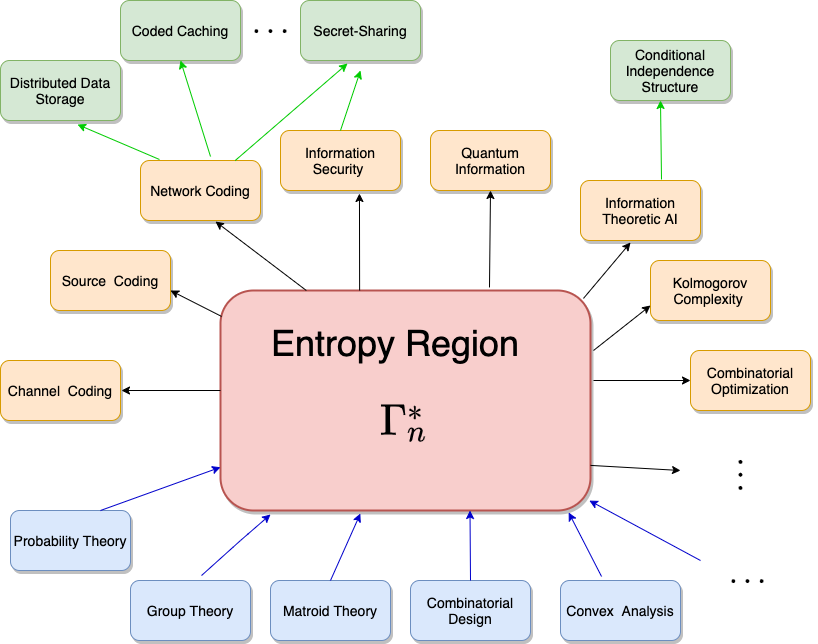
熵区域的刻画问题是信息论的基础核心问题，它决定着信息论中的其他领域，如信道编码、网络编码、信息论安全、信息论人工智能等的瓶颈问题的解决。熵区域的刻画问题还与量子信息、柯尔莫哥洛夫复杂度、群论等其他领域有对应关系。

 

 

  1. 拟阵熵函数

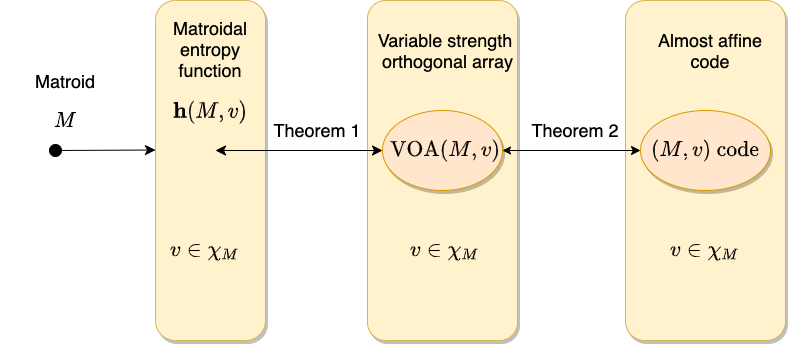
拟阵熵函数对信息论中的拟阵熵函数、拟阵论中的拟阵、组合设计中的变强度正交表，以及编码理论中的拟仿射码建立了一一对应关系，解析了4个领域中的内在逻辑关系，使得4个领域互通有无。由此产生的编码方案可以应用在网络编码、秘密分享、索引编码（index coding），以及局部修复码等领域。

  • 相关论文
  1. Q. Chen, M. Cheng and B. Bai, “Matroidal entropy functions: a quartet of theories of information, matroid, design and coding,”  Entropy, vol. 23:3, 1-11, 2021.
  2. Q. Chen, M. Cheng and B. Bai, “Matroidal entropy functions: characterizations, constructions and representations,” IEEE Int. Symp. Info. Theory, Espoo, Finland, June 2022.
  3. Q. Chen, M. Cheng and B. Bai, “Matroidal entropy functions: characterizations, constructions and representations,” in IEEE Trans. Inf. Theory vol. 71, no. 4. pp. 3237-3249 Apr. 2025 
  • 相关项目
  1. 阶数不大于6的拟阵熵函数的刻画 自由探索项目 6万 主持 2021-2022
  2. 大规模随机多址接入理论与技术研究 国家自然科学基金重点项目 299万 参与 2022-2026
  3.  拟阵熵函数的刻画及其在网络编码等领域中的应用 国家自然科学基金面上项目  51万 主持 2025-2028

  1. 信息论人工智能

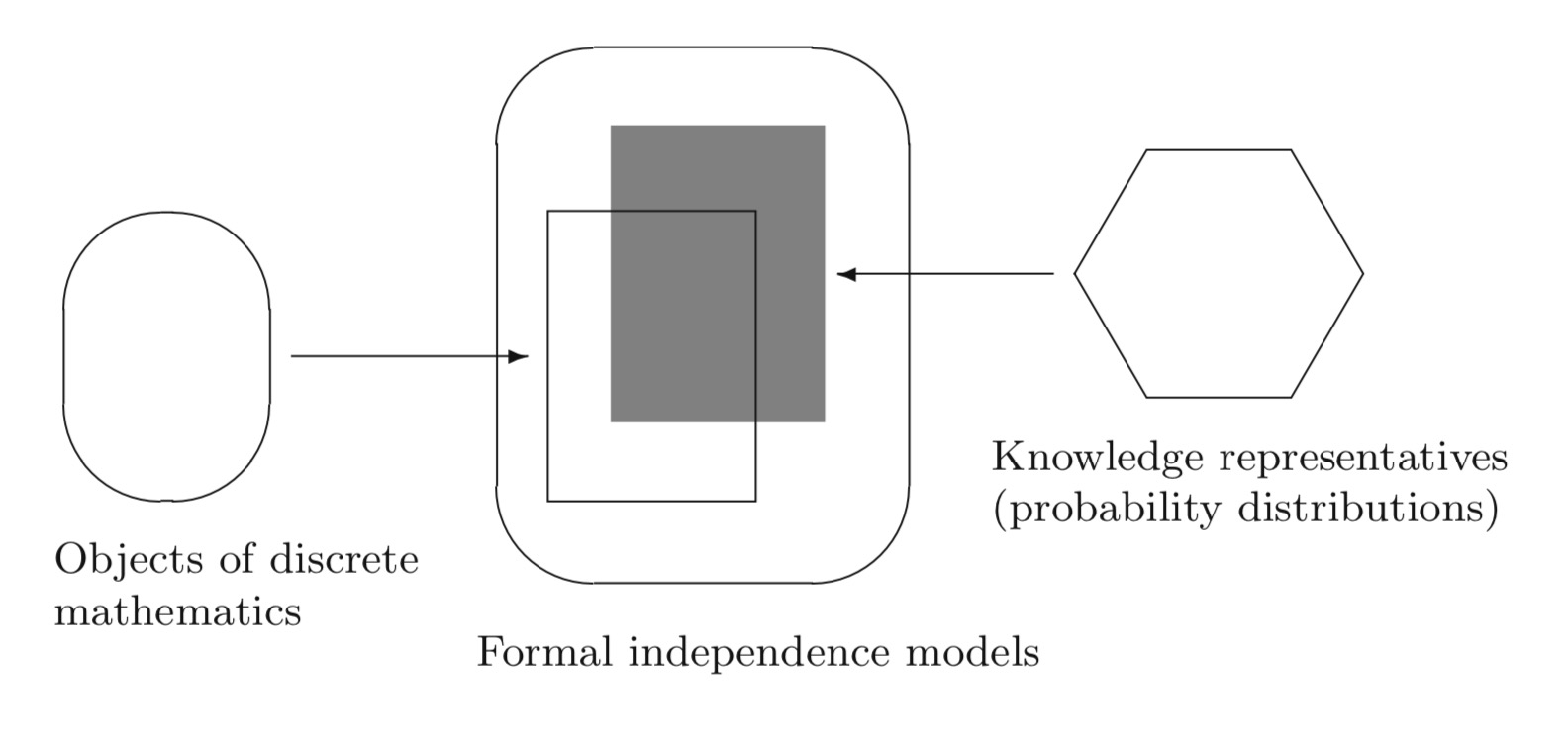
条件独立与条件相关、马尔科夫性等信息论问题在当今的人工智能领域有重要应用。

  • 相关论文
  1. Q. Chen, F. Cheng, T. Liu, and R. W. Yeung, “A marginal characterization of entropy functions for conditional mutually independent random variables (with application to wyner’s common information),” in IEEE Int.Symp. Info. Theory, Hong Kong, China June 2015.
  2. R. W. Yeung, A. Al-Bashabsheh, C. Chen, Q. Chen and P. Moulin, “On Information-Theoretic Characterizations of Markov Random Fields and Subfields,”  IEEE Int. Symp. Info. Theory, Aachen, Germany, June 2017.
  3. R. W. Yeung, A. Al-Bashabsheh, C. Chen, Q. Chen and P. Moulin, “On Information-Theoretic Characterizations of Markov Random Fields and Subfields,”  IEEE Trans. Inf. Theory, vol.65, no. 3, pp. 1493-1511, Mar. 2019.
  4. T. H. Chan, Q. Chen and R. W. Yeung,  “Characterisation of conditional independence structures for polymatroids using vanishing sets,” Kybernetika (Prague) 56(6), 1022–1044 (2020). 
  • 相关项目
  1. 熵区域的对称性及其应用 新教师基金 6万 主持 2019-2020
  2. 熵区域的对称性及其在马尔科夫随机域与网络 国家自然科学基金面上项目 61 万 主持 2020-2023

  1. 多拟阵区域面上的熵函数刻画

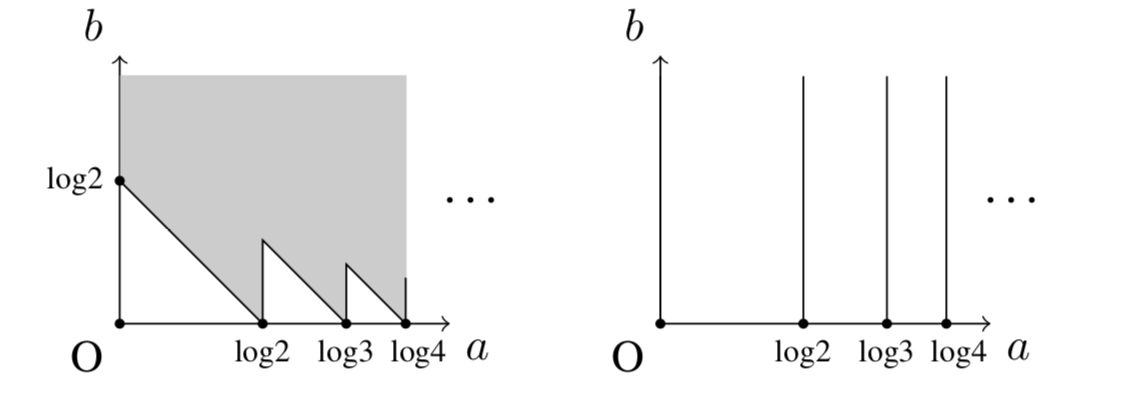
通过在多拟阵区域添加边界上的限制，刻画相应的熵函数。多拟阵面上的熵函数的刻画既与信息论人工智能相关，也构建了新的组合设计结构。

  • 相关论文

  1. Q. Chen* and R. W. Yeung, “Characterizing the entropy function region via extreme rays,”  IEEE Info. Theory Workshop, Lausanne, Switzerland Sep. 2012.

  2. Q. Chen*, F. Cheng, T. Liu, and R. W. Yeung, “A marginal characterization of entropy functions for conditional mutually independent random variables (with application to wyner’s common information),” in IEEE Int.Symp. Info. Theory, Hong Kong, China June 2015.

  3. S. Liu（2022级硕士研究生，发表该论文时为研一） and Q. Chen*,“Entropy functions on two-dimensional faces of polymatroidal region of degree four,” IEEE Int. Symp. Info. Theory, Taipei, China, June 2023.

  4. S. Liu, and Q. Chen*, “Entropy functions on two-dimensional faces of polymatroidal region of degree four: Part I: Problem formulation and graph coloring approach,” IEEE Trans. Inf. Theory, vol 72, no. 2, pp. 876-900, Feb, 2026.

  5. S. Liu, Q. Chen*, and M. Cheng, “Entropy functions on two-dimensional faces of polymatroidal region of degree four: Part II: Information theoretic constraints breed new combinatorial structures,” to appear in IEEE Trans. Inf. Theory.

  6.  K. He and Q. Chen* ``Entropy Functions on Two-Dimensional Faces of Polymatroid Region with One Extreme Ray Containing Rank-One Matroid'', IEEE Int.Symp. Info. Theory, Guangzhou, China, July 2026.

  • 相关项目
  1.  拟阵熵函数的刻画及其在网络编码等领域中的应用 国家自然科学基金面上项目  51万 主持 2025-2028            

  1. 熵区域的对称性

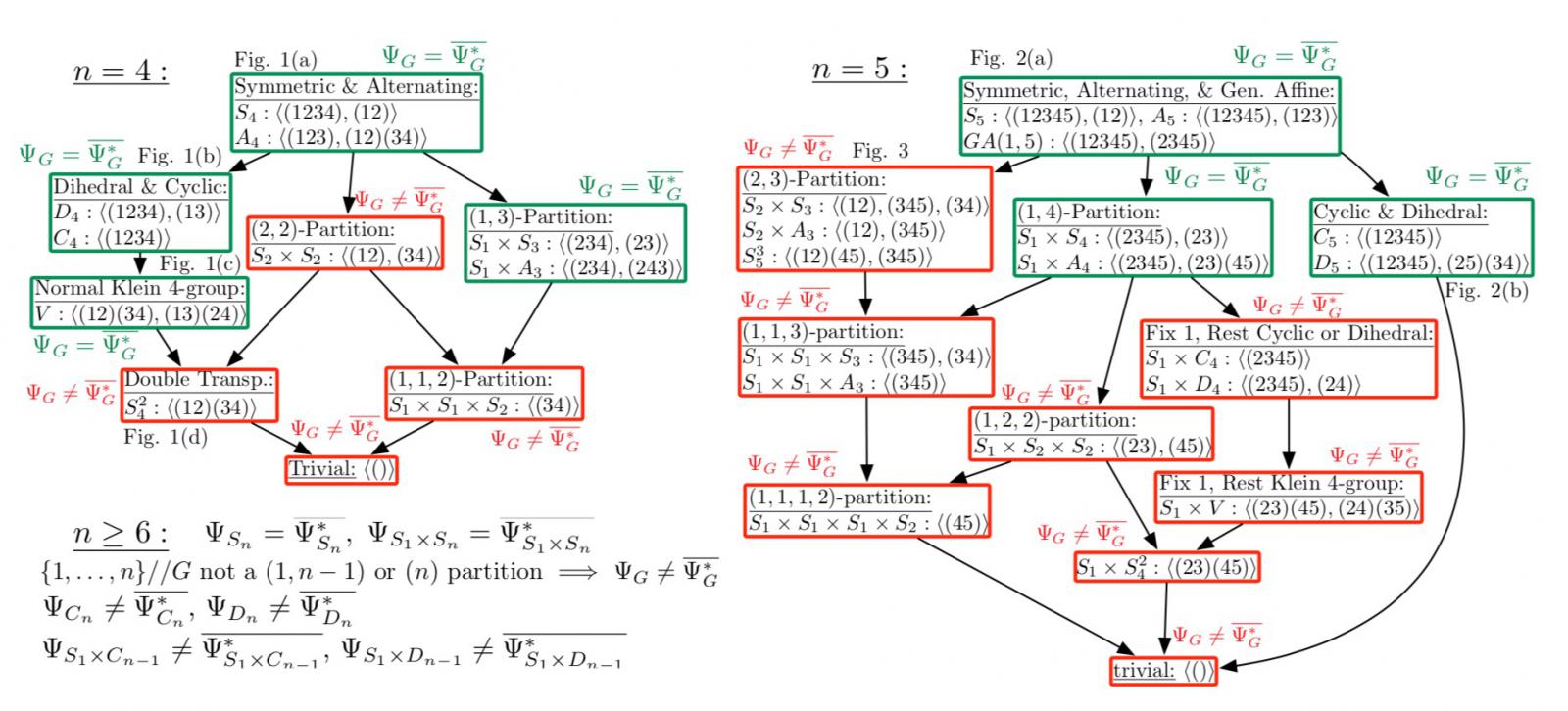
利用对称性刻画熵函数是刻画熵函数的又一方案。对称熵函数对于具有对称结构的信息论问题具有指导意义。

  • 相关论文：
  1. Q. Chen and R. W. Yeung,  "Two-Partition-Symmetrical Entropy Functions," IEEE Info. Theory Workshop, Seville, Spain, Sept. 2013.
  2. Q. Chen and R. W. Yeung,  "Partition-Symmetrical Entropy Functions," IEEE Trans. Inf. Theory vol. 62, no. 10, pp.5385–5402., Oct. 2016

  3. Apte, Q. Chen and J. W. Walsh, "Symmetries in the entropy space," IEEE Info. Theory Workshop, Cambridge, UK, Sept. 2016.

  4. Z. Li,（2023级硕士研究生，发表该论文时为研一） S. Liu and Q. Chen* ''Symmetric Entropy Regions of Degrees Six and Seven'',  IEEE Int.Symp. Info. Theory, Athens, Greece July 2024.

  • 相关项目
  1. 熵区域的对称性及其应用 新教师基金 6万 主持 2019-2020
  2. 熵区域的对称性及其在马尔科夫随机域与网络 国家自然科学基金面上项目 61 万 主持 2020-2023

________________________________________________________________________________________________________________________________________________________________

 

  1. 零差错容量问题

  • 相关论文：
  • Q. Cao and Q. Chen*, "On Zero-Error Capacity of \'One-Edge\' Binary Channels with Two Memories," IEEE Int. Symp. Info. Theory, Espoo, Finland, June 2022.
  • Q.Cao, Q. Chen*, B. Bai "On Zero-Error Capacity of Graphs with One Edge", IEEE Trans. Inf. Theory vol. 71, no. 5, pp.3350 - 3359, May, 2025
应用类型的课题：

BATS码问题

与创业公司安眺科技保持长期合作

版权声明
未经西安电子科技大学以及个人主页教师本人许可，不得复制、转载和传播本页内容，禁止用于任何商业用途。如需转载请征得主页所有者同意，并附上主页链接！
更新
技术支持：电院网络中心陕ICP备05016463号-3© 2026 西安电子科技大学